https://www.acmicpc.net/problem/3584
# 1번 풀이
T=int(input()) # 테스트 케이스의 개수 T
for _ in range(T):
# 1.입력
N=int(input()) # 전체 노드의 수 N
parent=[0]*(N+1)
for _ in range(N-1):
u,v=map(int,input().split())
parent[v]=u
A,B=map(int,input().split())
# 2.자료형 정의
ancestors=set()
# 3.알고리즘
# 3-1. A 조상 찾기
while A:
ancestors.add(A)
A=parent[A]
# 3-2. B 조상이 ancestors 안에 있는지 확인하기
while B not in ancestors:
B=parent[B]
# 4.출력
print(B)해당 문제는 LCA 문제이긴하지만 LCA 알고리즘 없이도 다음과 같이 풀 수 있었다.
처음에는 백준의 11437번 문제와 비슷하다고 생각하여 다음과 같이 풀이하였다.
2025.12.12 - [coding test/Baekjoon] - [Python] 11437번 LCA
[Python] 11437번 LCA
https://www.acmicpc.net/problem/11437import syssys.setrecursionlimit(int(1e5)) #런타임 오류 피하기N=int(input()) # 노드 개수# 그래프 정보 저장하기graph=[[] for _ in range(N+1)]for _ in range(N-1): v,u=map(int,input().split()) graph[v].
wish404.tistory.com
해당 문제에서는 이전의 11437번 문제와 달리 1번 노드만이 루트가 되는 것이 아니기 때문에
각 parent를 저장하고 parent가 0인 곳을 찾는 노가다로 루트 노드를 찾도록 코드를 짰다...
# 2번 풀이 -> 루트 찾기
import sys
sys.setrecursionlimit(int(1e5)) #런타임 오류 피하기
def dfs(x,d):
visited[x]=True
depth[x]=d
for y in graph[x]:
if not visited[y]:
dfs(y,d+1)
T=int(input()) # 테스트 케이스의 개수 T
for _ in range(T):
# 1.입력
N=int(input()) # 전체 노드의 수 N
graph=[[] for _ in range(N+1)]
parent=[0 for _ in range(N+1)]
for _ in range(N-1):
u,v=map(int,input().split())
graph[u].append(v)
graph[v].append(u)
parent[v]=u
A,B=map(int,input().split())
# 2.자료형 정의
depth=[0 for _ in range(N+1)]
visited=[0 for _ in range(N+1)]
# 3.알고리즘
# 3-1.root 찾기 / 깊이 구하기
for x in range(1,N+1):
if parent[x]==0:
dfs(x,0)
break
# 3-2. 깊이 맞추기
while depth[A]!=depth[B]:
if depth[A]>depth[B]:
A=parent[A]
else:
B=parent[B]
# 3-3. 공통 부모 구하기
while A!=B:
A=parent[A]
B=parent[B]
# 4.출력
print(A)
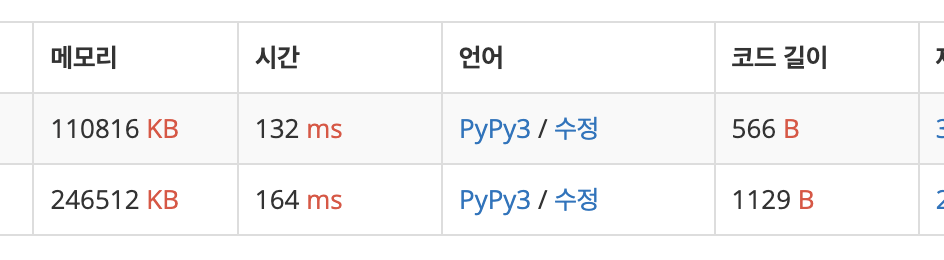
코드를 실행했을 때 1번 풀이의 메모리가 2번 풀이의 절반인 것을 볼 수 있다.
키워드에 집중하여 풀이하기 보다는 어떻게 하면 효율적으로 문제를 풀 수 있는지를 고민하는 자세를 기를 필요가 있음을 배웠다.
'coding test > Baekjoon' 카테고리의 다른 글
| [Python] 5430번. AC (0) | 2025.12.20 |
|---|---|
| [Python] 11438번 LCA 2 (0) | 2025.12.15 |
| [Python] 11437번 LCA (0) | 2025.12.12 |
| [Python] 1753번 최단경로 (0) | 2025.10.15 |
| [Python] 1715번 카드 정렬하기 (2) | 2025.08.30 |
