최소 공통 조상란?
최소 공통 조상(LCA) 문제는 두 노드의 공통된 조상 중에서 가장 가까운 조상을 찾는 문제
ex) 8번 노드와 15번 노드의 최소 공통 조상은 2번 노드이다.
ex) 3번 노드와 15번 노드의 최소 공통 조상은 1번 노드이다.

최소 공통 조상(LCA) 알고리즘 [기본]
- 모든 노드에 대한 깊이(depth) 계산
- 두 노드의 깊이(depth)가 동일하도록 거슬러 올라감
- 이후 부모가 같아질 때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라감



기본적인 최소 공통 조상(LCA) 알고리즘 구현 : Python
https://www.acmicpc.net/problem/11437
# 기본적인 LCA 알고리즘
import sys
sys.setrecursionlimit(int(1e5)) #런타임 오류 피하기
n=int(input())
parent=[0]*(n+1) # 부모 노드 정도
d=[0]*(n+1) # 각 노드까지의 깊이
c=[0]*(n+1) # 각 노드의 깊이가 계산되었는지 여부
graph=[[] for _ in range(n+1)] # 그래프(graph) 정보
for _ in range(n-1):
a,b=map(int,input().split())
graph[a].append(b)
graph[b].append(a)
# 루트 노드부터 시작하여 깊이(depth)를 구하는 함수
def dfs(x,depth):
c[x]=True
d[x]=depth
for y in graph[x]:
if c[y]: # 이미 구했다면 넘기기
continue
parent[y]=x
dfs(y,depth+1)
# A와 B의 최소 공통 조상 찾는 함수
def lca(a,b):
# 먼저 깊이(depth)가 동일하도록
while d[a]!=d[b]:
if d[a]>d[b]:
a=parent[a]
else:
b=parent[b]
# 노드가 같아지도록
while a!=b:
a=parent[a]
b=parent[b]
return a
dfs(1,0) # 루트 노드는 1번 노드
m=int(input())
for _ in range(m):
a,b=map(int,input().split())
print(lca(a,b))
❗ 하지만 이 방식은 쿼리(질의)가 많을 때 너무 느림 ⇒ O(N) per query
매 쿼리마다 부모 방향으로 거슬러 올라가기 위해 최악의 경우 O(N)의 시간 복잡도 요구
따라서 모든 쿼리를 처리할 때의 시간 복잡도는 O(NM)
최소 공통 조상(LCA) 알고리즘 [심화]
그렇다면 시간 복잡도를 줄이기 위해서는?
→ 그래서 보통 이진 리프팅(Binary Lifting) 을 사용해 O(log N) 으로 빠르게 LCA를 찾는다.
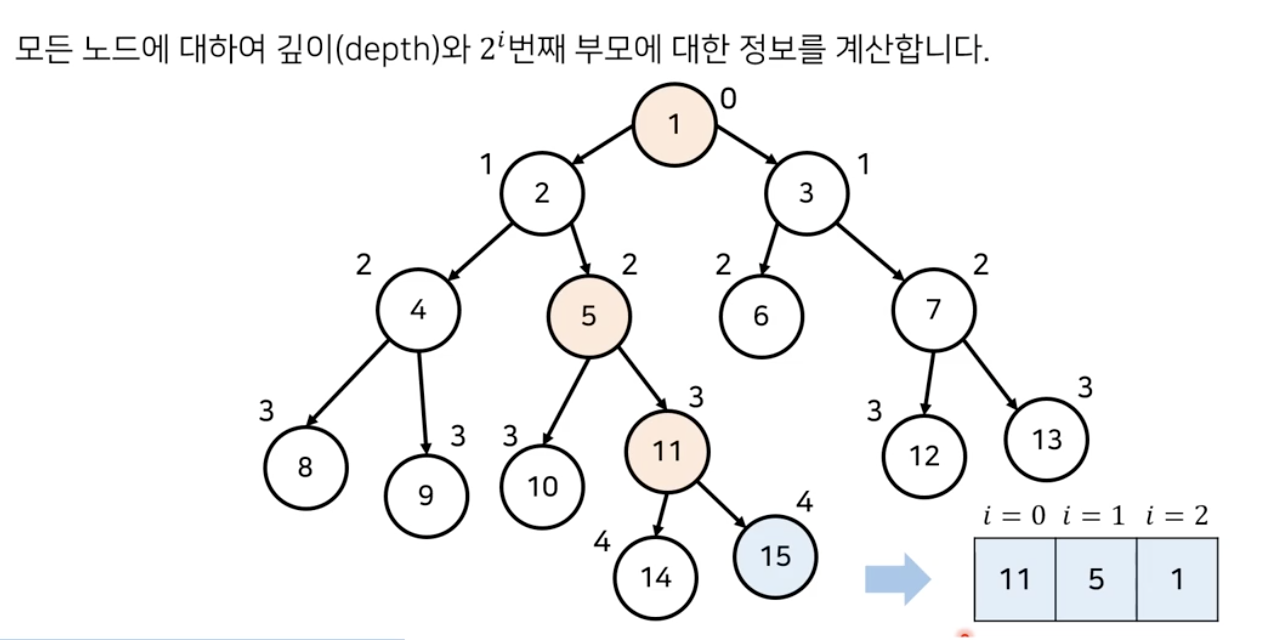
즉, 각 노드 v에 대하여 2^k번째 조상(parent[k][v])를 미리 저장해둔다.
예)
- parent[v][0] = v의 2⁰=1번째 조상 (= 바로 부모)
- parent[v][1] = v의 2¹=2번째 조상
- parent[v][2] = v의 2²=4번째 조상
- parent[v][3] = 8번째 조상
…
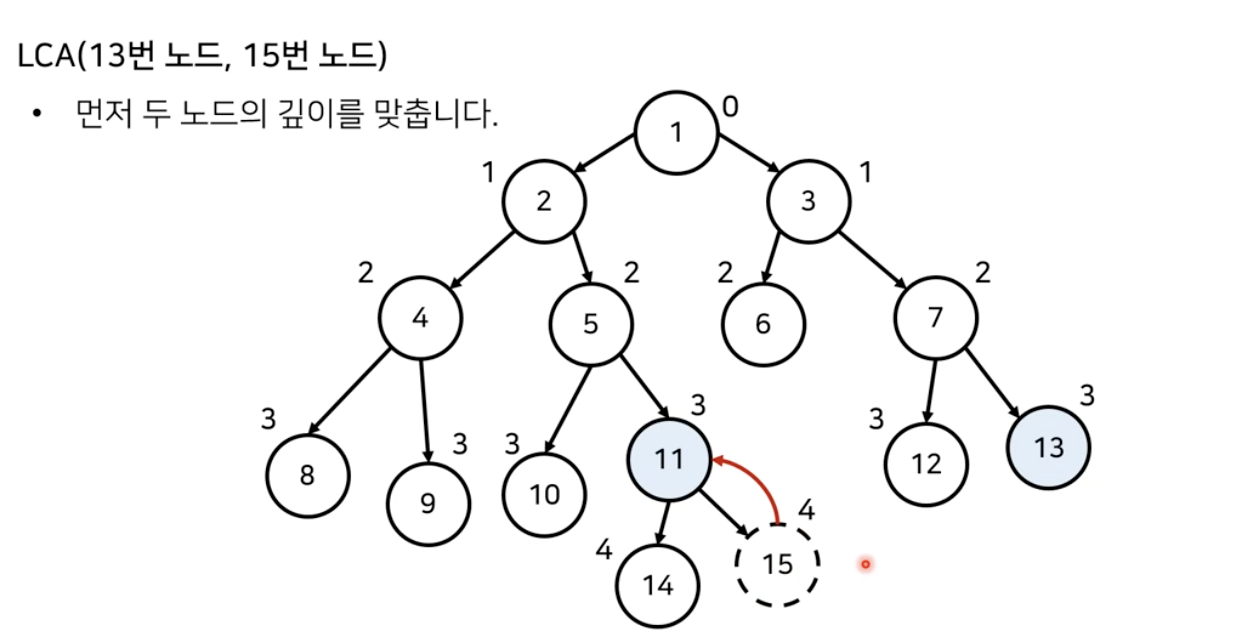
동작 과정은 다음과 같다.
- 먼저 두 노드의 깊이를 맞춘다.
- 이후 거슬러 올라간다.


❗ 개선된 코드는
- 다이나믹 프로그래밍(DP)를 이용해 시간 복잡도를 계선할 수 있음
- 세그먼트 트리를 이용하는 방법도 존재
- 매 쿼리마다 부모를 거슬러 올라가기 위해 O(logN)의 시간 복잡도 필요
- 따라서 모든 쿼리를 처리할 때의 시간 복잡도는 O(MlogN)
개선된 최소 공통 조상(LCA) 알고리즘 구현 : Python
https://www.acmicpc.net/problem/11438
# 시간 복잡도가 개선된 LCA 알고리즘
import sys
input=sys.stdin.readline
sys.setrecursionlimit(int(1e5)) #런타임 오류 피하기
LOG=21 # 2^20=1,000,000
n=int(input())
parent=[[0]*LOG for _ in range(n+1)] # 부모 노드 정보
d=[0]*(n+1) # 각 노드까지의 깊이
c=[0]*(n+1) # 각 노드의 깊이가 계산되었는지 여부
graph=[[] for _ in range(n+1)] # 그래프 정보
for _ in range(n-1):
a,b=map(int,input().split())
graph[a].append(b)
graph[b].append(a)
# 루트 노드부터 시작하여 깊이(depth)를 구하는 함수
def dfs(x,depth):
c[x]=True
d[x]=depth
for y in graph[x]:
if c[y]: # 이미 깊이를 구했다면 넘기기
continue
parent[y][0]=x
dfs(y,depth+1)
# 전체 부모 관계를 설정하는 함수
def set_parent():
dfs(1,0) # 루트 노드는 1번 노드
for i in range(1,LOG):
for j in range(1,n+1):
parent[j][i]=parent[parent[j][i-1]][i-1]
# A와 B의 최소 공통 조상을 찾는 함수
def lca(a,b):
# b가 더 깊도록 설정
if d[a]>d[b]:
a,b=b,a
# 먼저 깊이(depth)가 동일하도록
for i in range(LOG-1,-1,-1):
if d[b]-d[a]>=(1<<i):
b=parent[b][i]
# 부모가 같아지도록
if a==b:
return a
for i in range(LOG-1,-1,-1):
# 조상을 향햐 거슬러 올라가기
if parent[a][i]!=parent[b][i]:
a=parent[a][i]
b=parent[b][i]
# 이후에 부모가 찾고자 하는 조상
return parent[a][0]
set_parent()
m=int(input())
for i in range(m):
a,b=map(int,input().split())
print(lca(a,b))
[Reference]
'coding test > Algorithm' 카테고리의 다른 글
| 최단 경로 (1) | 2025.08.31 |
|---|---|
| 최소 신장 트리(MST) (0) | 2025.08.31 |
| Dynamic Programming - 기초 (0) | 2025.05.17 |
